Hi, welcome to the 6th article of this blog.
In this blog post, the breakout example from the last Post has been improved, giving it more features:
- The Paddle and Blocks have rounded edges. The ball bounces of them depending on the surface normal where it hits.
- The blocks are fading out when destroyed.
- The paddle can shot to destroy blocks. When the game starts one shot is available, shots can be gained by destroying green blocks.
- The game is aware when the player lost or won and displays this information when the game ends.
But that is not all! Instead of using the simple Coroutines we are now using a full blown FRP library called netwire. But more about that later, here is the preview. As alwyas you have to click the canvas to get input focus. If you are not viewing this blog article on blogspot and the application does not work, try the original aricle page.
I had a lot of help over the haskell beginners mailing list. I will try to add links to the specific topics whenever I am writing something I had help with.
As a final note before I start: Being a haskell beginner, I might not do everything here the best way. I encourage you to comment if you think something could be done better! Of course, I also encourage you to comment if you have any questions.
About Netwire
Netwire is a arrowized functional reactive programming (AFRP) library for haskell and the version 4 of the library has recently been released on hackage. Since it uses Arrows, some of the things we did with Coroutines can be done the same way with netwires, but it has tons of other features. Here is a short introduction to netwire, but I will try to explain all the features when I use them.
Also I will explain some of netwires usage here, this is by no means a complete tutorial to netwire. One obvious reason for this is, that I myself do not (yet?) understand all the features and Ideas of netwire (remember, I am still a haskell beginner doing this for my own education). Maybe some of this will be useful for someone wanting to start with netwire.
To install netwire, just type
haste-inst install netwireThis will most likely fail on lifted-base and time. There is a (potentially dangerous) workaround here, that should work for now.
New Javascript functions
To Draw a rounded rectangle a new function "fillRoundedRect" is defined in JavaScript.hs. Also a new type for Colors has been added:
data Color = Color {red :: Double, green :: Double, blue :: Double, alpha :: Double}"jsFillColor" now takes this as argument instead of a string.
Collision detection
See here for the complete code. We want to represent our objects as Circles (the ball, bullets) and rounded rectangles (the paddle, blocks), so we define data structures for this:
-- Information about collision
type Vector = (Double, Double) -- thanks to vector-space we can do ^+^ and similar
data Collision = Collision { normal :: Vector } deriving (Show)
type Radius = Double
data Circle = Circle { circlePos :: Vector, circleRadius :: Radius}
data Rectangle = Rectangle Vector Vector
data RoundedRect = RoundedRect { rectMin :: Vector, rectMax :: Vector, rectRadius :: Radius}The Collision information now contains the normal of the collision. This is needed to correctly bounce the ball.
For convenience in the usage of the collision functions, we will define type classes for the objects having the shape of a circle or a rounded rectangle:
class CircleShaped a where
circle :: a -> Maybe Circle
class RoundedRectShaped a where
roundedRect :: a -> Maybe RoundedRect
instance CircleShaped Circle where
circle c = Just c
instance RoundedRectShaped RoundedRect where
roundedRect r = Just rThis allows us to apply the collision functions directly to our game objects (when they are instances of the corresponding class) without always explicitly extracting the shape. In other words, instead of writing:
circleRectCollision (ballCircle ball) (blockRect block)we can write
circleRectCollision ball blockThe type classes return maybe types, because some objects might become "shapeless" and should not collide (for example a block that is fading out).
Ok, the first thing we need is a collision between circles
import Control.Monad
circleCollision :: (CircleShaped a, CircleShaped b) => a -> b -> Maybe Collision
circleCollision a b = do
(Circle p1 r1) <- circle a
(Circle p2 r2) <- circle b
let centerDiff = p2 ^-^ p1
guard (centerDiff <.> centerDiff <= (r1 + r2) * (r1 + r2))
return $ Collision $ normalized centerDiffIt returns a "Maybe Collision" because a collision might not take place. Notice the "do" notation. We are in the "Maybe" monad, which causes the function to automatically return Nothing if one of out circle shapes return Nothing (if you do not understand, see here). So we are getting the vector between the center positions and testing its square against the square of the sums of the radian of the circles. The guard function (from Control.Monad) causes the monad to return with "Nothing" if the circles are not close enough. Then we return the normalized vector as the normal. Notice that the normal always points from the first circle to the second.
As a helper function, we test if a point is inside a rectangle:
pointInRectangle :: Vector -> Rectangle -> Bool
pointInRectangle (px,py) (Rectangle (minX,minY) (maxX,maxY))
| px > maxX = False
| px < minX = False
| py > maxY = False
| py < minY = False
| otherwise = TrueThat should be clear.
So how do we test a circle against a rounded rectangle? A rounded rectangle is rectangle where the corners have been replaced by quarter circles. We have do test against these circles or the "inner" rectangle depending on where the colliding circle is, see this picture:
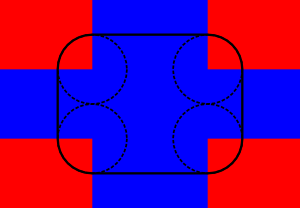
Areas of rounded rectangle
When the center of the colliding circle is in one of the red areas, collision testing is done with the corresponding corner circles. Otherwise collision is done against the "unrounded" rectangle (which is the same as rounded rectangle when we not in one of the red areas). The normal is then determined by the normal of the closest rectangle side. Here is the code:
circleRoundedRectCollision :: (CircleShaped a, RoundedRectShaped b) => a -> b -> Maybe Collision
circleRoundedRectCollision c r = do
circle <- circle c
rect <- roundedRect r
circleRoundedRectCollision' circle rect
where
circleRoundedRectCollision' circle@(Circle (cx,cy) cr) (RoundedRect (minX,minY) (maxX,maxY) rr)
--test the corners
| cx <= innerMinX && cy <= innerMinY = circleCollision (Circle (innerMinX, innerMinY) rr) circle
| cx >= innerMaxX && cy <= innerMinY = circleCollision (Circle (innerMaxX, innerMinY) rr) circle
| cx >= innerMaxX && cy >= innerMaxY = circleCollision (Circle (innerMaxX, innerMaxY) rr) circle
| cx <= innerMinX && cy <= innerMinY = circleCollision (Circle (innerMinX, innerMaxY) rr) circle
-- test if collision with rectangle occured
| not $ pointInRectangle (cx,cy) (Rectangle ((minX-cr), (minY-cr)) ((maxX+cr), (maxY+cr))) = Nothing
-- collision definitly occured, find correct normal
| otherwise = Just $ fst $ minimumBy (\(_,a) (_,b) -> compare a b)
[
(Collision (-1.0,0.0), cx - minX),
(Collision (1.0, 0.0), maxX - cx),
(Collision (0.0,-1.0), cy - minY),
(Collision (0.0, 1.0), maxY - cy)
]
where
innerMinX = minX + rr
innerMinY = minY + rr
innerMaxX = maxX - rr
innerMaxY = maxY - rrI am a bit unhappy that I have to define the inner function "circleRoundedRectCollision'", but I do not know how else I could use this nice pattern guards.
Wire helpers
To handle bullets and blocks we need some way to manage a set of objects where objects can be removed. For this I got a lot of help here and here. The code is here. Let's look at the type of a wire:
data Wire e m a bThe m parameter is the underlying monad. We will set it to Identity and be fine with it. "a" is the input type. Quoting from here: From these inputs it (the wire)
- either produces an output value of type "b" or inhibits with a value of type "e",
- produces a new wire of type Wire e m a b.
When a wire produces, it is the same as our Coroutines producing output. The possibility that a wire can inhibit is often used to switch to different wires. See here. We will explore this possibility a little bit further down.
dynamicSet
When a wire inhibits, there are several combinators which allows to switch to other wires (permanently or just for one instance). Here inhibiting wires will be removed from the set. To create new wires a creator function and an additional input will be used.
dynamicSet :: (Monad m) => (c -> Wire e m a b) -> [Wire e m a b] -> Wire e m (a, [c]) [b]
dynamicSet creator ws' = mkGen $ \dt (i,new) -> do
res <- mapM (\w -> stepWire w dt i) ws'
let filt (Right a, b) = Just (a,b)
filt _ = Nothing
resx = mapMaybe filt res
return (Right $ (fmap fst resx), dynamicSet creator $ (fmap snd resx) ++ (map creator new))mkGen is passed a function that is turned into a wire. The parameters for this function are the time delta (dt) and the input (i,new) of the wire. We use the do notation because we are in the inner Monad "m" (of which we know nothing but that it is a monad). After we stepped all wires ("stepWire" steps a wire ,see netwire tutorial) we filter those that produced (by returning a right value) and return there outputs as list. The new wire is again a dynamics set with the ramaing wires and the newly created ones using the creator function.
dynamicSetMap
To use dynamic set in the breakout game, we assign each wire in the set a unique key (Int) and change the input to a Map that maps from the key to the input values of the individual wires. Since a map lookup may fail, the input of the wires will be Maybes.
To archive this we define a wire that takes a list as inputs and pairs it with a given (infinite) list (which will be our keys):
-- queue for the objects in the list given as parameter
-- The Int argument says how many objects should be returned
staticQueue :: (Monad m) => [a] -> Wire e m Int [a]
staticQueue set = unfold give set
where
give s n = (take n s, drop n s)
-- Pairs the input list with the given list, which is assumed to be infinite
pairListsWith :: (Monad m) => [p] -> Wire e m [a] [(p,a)]
pairListsWith pairs = proc as -> do
p <- staticQueue pairs -< length as
returnA -< zip p asusing these wires we define dynamicSetMap:
dynamicSetMap :: (Monad m) => (c -> Wire e m (Maybe a) b) -> [Wire e m (Maybe a) b] -> Wire e m (M.Map Int a, [c]) [(Int,b)]
dynamicSetMap creator ws = dynamicSet creator' ws' . (second $ pairListsWith restKeys)
where
wireWithLookupAndKey :: (Monad m) => Int -> Wire e m (Maybe a) b -> Wire e m (M.Map Int a) (Int,b)
wireWithLookupAndKey i w = (pure i) &&& (w . (arr (M.lookup i)))
keys = [0,1..]
restKeys = drop (length ws) keys
ws' = map (uncurry wireWithLookupAndKey) $ zip keys ws
creator' (i,c) = wireWithLookupAndKey i (creator c)shrinking and shrinkingMap
Since blocks can not be created, only destroyed, we define a simplified version of dynamicSet and dynamicSetMap where no new wires can be created.
-- same as dynamicSet, only that it can not grow
shrinking :: (Monad m) => [Wire e m a b] -> Wire e m a [b]
shrinking ws = dynamicSet undefined ws <<< arr (\a -> (a,[]))
-- same as dynamicSetMap, only that it can not grow
shrinkingMap :: (Monad m) => [Wire e m (Maybe a) b] -> Wire e m (M.Map Int a) [(Int,b)]
shrinkingMap ws = dynamicSetMap undefined ws <<< arr (\a -> (a,[]))To conclude these helper wires, I am not sure if these are the best choices but they work for now.
The Game
Finally we are ready to define the game itself! The code is here.
Input
In difference to the last post, we will step the wire on every input event. An input event will be a keyboard event or an "Update" event which causes the main wire to update all game objects.
data InputEvent = KeyUp Int | KeyDown Int | Update
deriving (Eq)Data objects
Here are the data objects defining the state of the game:
-- state of game objects
data Paddle = Paddle { xPos :: Double }
data Gun = Gun { ammo :: Int }
data Ball = Ball { ballPos :: Vector,
ballSpeed :: Vector}
data Block = Block { blockType :: BlockType, blockPos :: Vector, blockState :: BlockState}
data BlockState = Alive Int | Dying Double
data BlockType = NormalBlock | PowerBlock deriving (Eq)
data Bullet = Bullet { bulletPos :: Vector }
data GameState = GameState {
paddle :: Paddle,
gun :: Gun,
ball :: Ball,
blocks :: [Block],
bullets :: [Bullet]}
| StartScreen StringThe StartScreen constructor of the GameState is to show a message when the game is not running (in the beginning and when the player won or lost). We gave the ball the ballSpeed property (which is not necessary for viewing the game state) because it will be needed outside the balls own wires later. You will see. The Double parameter for a Dying block is the fade level (going from 1.0 to 0.0 as the block is removed). A Block now also as a BlockType. A PowerBlock is a block that gives the player ammo when destroyed.
constants
A lot of constants follow which define the properties of the game
-- constants
screenWidth = 600.0
screenHeight = 400.0
paddleColor = Color 0.0 0.0 0.0 1.0
paddleYPos = screenHeight - paddleHeight
paddleHeight = 15.0
paddleWidth = 50.0
paddleRadius = 7.0
paddleSpeed = 7.0
initPaddleXPos = (screenWidth - paddleWidth) / 2.0
initPaddle = Paddle initPaddleXPos
initGun = Gun 1
ballColor = Color 1.0 0.0 0.0 1.0
ballRadius = 5.0
initBallSpeed = (3.0, -3.0)
initBallPos = (screenWidth / 2.0, screenHeight - 50.0)
initBall = Ball initBallPos initBallSpeed
blockWidth = 60.0
blockHeight = 20.0
blockRadius = 5.0
normalBlockColor = [Color 0.0 0.0 1.0 1.0, Color 0.0 0.0 0.5 1.0]
powerBlockColor = [Color 0.0 0.5 0.0 1.0]
initBlocks = [Block t (x,y) (Alive l) | x <- [20.0, 140.0, 240.0, 340.0, 440.0, 520.0], (y,t,l) <- [(60.0, PowerBlock, 1), (100.0, NormalBlock,2), (140.0,NormalBlock,1), (180.0,NormalBlock,2), (260.0,NormalBlock,2)]]
bulletRadius = 3.0
bulletSpeed = (0.0, -10.0)
bulletColor = Color 0.0 0.5 0.0 1.0
-- technical constants
leftKeyCode = 37
rightKeyCode = 39
startKeyCode = 13
fireKeyCode = 32
canvasName = "canvas4"The canvas name is the same name as defined in the outer html where the canvas is located.
Startup and key events
As said earlier, we step the main wire on every key event. But besides that the key event and startup functions look very similar to the last post. Also the drawing function has been extended to draw bullets and fading blocks. To produce the game state to draw, the wire is step with "Update". See here if you want to see the code.
Key events
In netwire an Event is a Wire that behaves as the identity wire when the event occurs and inhibits when the event does not occure. There are many functions to create events in netwire. Most require the inhibition type of the wire to be a monoid. That is very useful for switching on events. For now just accept that, you will see later.
So we create events that produce when the input event is a certain key down or release event:
keyPress :: (Monad m, Monoid e) => Int -> Event e m InputEvent
keyPress code = when (==KeyDown code)
keyRelease :: (Monad m, Monoid e) => Int -> Event e m InputEvent
keyRelease code = when (==KeyUp code)now we can write a wire that returns a different value depending on if a key is pressed:
import qualified Data.Function as F
valueFromKeyDown :: (Monad m, Monoid e) => Int -> a -> a -> Wire e m InputEvent a
valueFromKeyDown code upValue downValue = F.fix (\start ->
pure upValue . notE (keyPress code) -->
pure downValue . notE (keyRelease code) -->
start)- The "-->" operator is the infix version of "andThen". It takes two wires and behaves like the first until that inhibits. After that it behaves like the second.
- pure takes a value and makes a constant wire from it
- if you do not know fix, read here. Here it is used to loop back the chain of wires to the beginnig.
The paddle
The speed of the paddle is direct transformation of the input state while the paddle wire integrates the paddle speed bounding it the the limits of the screen.
paddleWire :: (Monad m, Monoid e) => Wire e m InputEvent Paddle
paddleWire = Paddle <$> (integralLim1_ bound initPaddleXPos <<< (paddleSpeedWire &&& pure ()))
where
bound _ _ pos = max 0.0 $ min (screenWidth-paddleWidth) pos
paddleSpeedWire :: (Monad m, Monoid e) => Wire e m InputEvent Double
paddleSpeedWire = (valueFromKeyDown leftKeyCode 0.0 (-paddleSpeed))
+
(valueFromKeyDown rightKeyCode 0.0 paddleSpeed)The ball
Similar as in the last Post, the ball moves with constant speed and reacts to collision events.
accum1Fold :: (Monad m) => (b -> a -> b) -> b -> Wire e m [a] b
accum1Fold f init = accum1 step init
where
step last as = foldl' f last as
ballSpeedWire :: (Monad m) => Wire e m [Collision] Vector
ballSpeedWire = accum1Fold (collide) initBallSpeed
where
collide v0 (Collision n) = v0 - (2.0 * (n <.> v0)) *^ n
ballWire :: (Monad m) => Wire e m [Collision] Ball
ballWire = (Ball <$> integral1_ initBallPos) . ballSpeedWire <*> ballSpeedWireNotice the use of accum1. In difference to accum, accum1 does not delay its output by one invocation. accum1Fold does the same as accum1 but takes a list as input over which it folds. Here it is used to fold over the incomming collision events.
What happens when the ball collides with an object? Assuming the collision is fully elastic, the velocity along the collision normal is inverted. The velocity (v0) along the collision normal (n) is <n,v0> (the scalar product of n and v0). Expressed with vector space, this is n <.> v0. To invert this part of v0, we have to substract this twice from v0. This gives us: v0 - (2.0 * (n <.> v0)) *^ n.
Blocks
A block behaves as its initial state, removing a live whenever it is hit (its input is not Nothing). When the lives are out, the block changes into the Dying state. And fades out in 30.0 "time units". Afterwards the block wire inhibts (so it is removed from the set).
blockWire :: (Monad m, Monoid e) => Block -> Wire e m (Maybe Collision) Block
blockWire init = while blockAlive . accum1 update init -->
Block (blockType init) (blockPos init) <$> (Dying <$> (pure 1.0) - (time / (pure 30.0))) . for 30.0
where
update old Nothing = old
update old@(Block _ _ (Alive l)) _ = old { blockState = Alive (l - 1) }
blockAlive (Block _ _ (Alive l)) = l > 0Notice the expression "(pure 1.0) - (time / (pure 30.0)))" for the fading level. We can use "-" and "/" because wires are members of the Fractional and Num type classes. We could even leave out the "pure" and write "(1.0) - (time / (30.0)))". At present this does not work with haste because "framRational" needs some not yet supported primOps (see here).
When a "PowerBlock" is destroyed, the player is supposed to gain ammo. Therefore there is a blockAmmoWire that returns the number of ammo the player should gain. For a normal block it returns always 0. For a PowerBlock it returns 0 except the moment the block is destoryed (the input is not Nothing).
blockAmmoWire :: (Monad m, Monoid e) => Block -> Wire e m (Maybe Collision) Int
blockAmmoWire (Block PowerBlock _ _) = (pure 0) . while (isNothing) --> once . (pure 1) --> pure 0
blockAmmoWire _ = (pure 0)
blockWithAmmoWire :: (Monad m, Monoid e) => Block -> Wire e m (Maybe Collision) (Int,Block)
blockWithAmmoWire b = blockAmmoWire b &&& blockWire bIsn't it nice how easily this can be expressed with "-->"?
Now we create a set of blocks using "shrinkingMap":
blocksWire :: (Monad m, Monoid e) => Wire e m (M.Map Int Collision) (Int,[(Int,Block)])
blocksWire = (shrinkingMap $ map blockWithAmmoWire initBlocks) >>> (arr reorder)
where
reorder as = (sum $ map (fst . snd) as, map (\j -> (fst j, snd $ snd j)) as)The output of "(shrinkingMap $ map blockWithAmmoWire initBlocks)" is [(id,(ammo,block))] where "id" is the id of the corresponding block, "ammo" the ammo given by the block and "block" its state.
But what we want is (sumAmmo, [(id,block)]) with sumAmmo being the sum over all ammo. That is what reaorder takes car of.
Bullets
Bullets simply move up while
- They do not collide
- They are not out of the screen
bulletWire :: (Monad m, Monoid e) => Bullet -> Wire e m (Maybe Collision) Bullet
bulletWire (Bullet init) = while bulletAlive . (Bullet <$> (pure bulletSpeed >>> integral1_ init)) . while (isNothing)
where
bulletAlive (Bullet (x,y)) = y > 0.0
bulletsWire :: (Monad m, Monoid e) => Wire e m (M.Map Int Collision,[Bullet]) [(Int,Bullet)]
bulletsWire = dynamicSetMap bulletWire []Gun
The gun gets a set of bullets as input (these are the fire requests) and an integer with the amount of new ammo. It outputs the bullets that really have been fired and the gun state
gunWire :: (MonadFix m) => Wire e m ([Bullet],Int) ([Bullet],Gun)
gunWire = proc (bs,new) -> do
rec
let fires = take ammo bs
ammo <- accum (+) (ammo initGun) -< new - (length fires)
returnA -< (fires,Gun ammo)Collecting collision information
We define some helper functions for collecting collisions betwen the ball, the paddle, the walls, blocks and bullets:
fromMaybeList :: Ord a => [(a,Maybe b)] -> M.Map a b
fromMaybeList [] = M.empty
fromMaybeList ((k,Nothing):xs) = fromMaybeList xs
fromMaybeList ((k,Just v):xs) = M.insert k v (fromMaybeList xs)
calcBallBlockColls :: Ball -> [(Int,Block)] -> M.Map Int Collision
calcBallBlockColls ball = fromMaybeList . map (\(id,block) -> (id,circleRoundedRectCollision ball block))
calcBallWallColls :: Ball -> [Collision]
calcBallWallColls (Ball (bx,by) _) = map snd $ filter (fst) $ [
(bx <= 0 , Collision (1.0 , 0.0)),
(bx >= screenWidth, Collision (-1.0, 0.0)),
(by <= 0 , Collision (0.0 , 1.0))
]
calcBallPaddleColls :: Ball -> Paddle -> [Collision]
calcBallPaddleColls b p =
maybeToList $ circleRoundedRectCollision b p
pairUp :: [a] -> [b] -> [(a,b)]
pairUp as bs = [(a,b) | a <- as, b <- bs]
calcBlockBulletColls :: [(Int,Block)] -> [(Int,Bullet)] -> (M.Map Int Collision,M.Map Int Collision)
calcBlockBulletColls blocks bullets = foldl' buildColls (M.empty, M.empty) $ pairUp blocks bullets
where
buildColls (blList, buList) ((blId,block), (buId, bullet)) = case circleRoundedRectCollision bullet block of
Nothing -> (blList, buList)
Just c -> (M.insert blId c blList, M.insert buId c buList)Putting it all together, the main wire
Switching game state
Let's first look at the outer wire, that manages when the game starts and when to show the start screen. It should behave like this:
- In the beginnig it shows "Press Enter to start (click canvas to focus)". When the user pressed enter the game is started.
- When the player looses, is shows "Sorry, you loose! Press Enter to restart." and lets the user press enter to restart.
- Similar when the player wins, with the message "Congratulations, you won! Press Enter to restart."
So when the game ends we need to switch differently depending on if the game was lost or won. Remember that the inhibition if wires can be used to switch wires (for example with "-->"). If we want to have different wire we have to encode this in the inhibition Type (see also this thread):
data GameEnd = Win | Loose | None
instance Monoid GameEnd where
mempty = None
mappend x None = x
mappend None x = x
mappend _ Win = Win
mappend Win _ = Win
mappend _ _ = Loose
type MainWireType = Wire GameEnd Identity InputEvent (Maybe GameState)The inhibition value must be a Monoid, because that is what most switches and events require. Now we can use this with switchBy:
mainWire = switchBy start (start None)
where
start None = startScreenWire "Press Enter to start (click canvas to focus)" --> mainGameWire
start Win = startScreenWire "Congratulations, you won! Press Enter to restart." --> mainGameWire
start Loose = startScreenWire "Sorry, you loose! Press Enter to restart." --> mainGameWireNow the mainGameWire only has to inhibit when the game is lost, or won. This is done with these wires:
looseWire :: (Monad m) => Wire GameEnd m Ball Ball
looseWire = unless ballOut --> inhibit Loose
where
ballOut (Ball (x,y) _) = y > screenHeight
winWire :: (Monad m) => Wire GameEnd m [Block] [Block]
winWire = (once --> unless null) --> inhibit WinThe "once" in the win wire is necessary because in the first invocation of the main wire there are no blocks.
The main game
This is the only place, where we use arrow syntax:
mainGameWire :: MainWireType
mainGameWire = proc input -> do
paddle <- paddleWire -< input
let newFR old
| input == Update = []
| input == KeyDown fireKeyCode = (createBullet paddle):old
| otherwise = old
fireRequests <- accum (flip ($)) [] -< newFR
if input == Update then do
rec
let validCollDir (Collision n) = n <.> ballSpeed oldBall < 0.0
ballBlockColls = M.filter validCollDir $ calcBallBlockColls oldBall oldBlocks
ballWallColls = calcBallWallColls oldBall
ballPaddleColls = filter validCollDir $ calcBallPaddleColls oldBall paddle
(blockBulletColls,bulletBlockColls) = calcBlockBulletColls oldBlocks oldBullets
ball <- ballWire -< ballWallColls ++ ballPaddleColls ++ (M.elems ballBlockColls)
oldBall <- delay initBall -< ball
_ <- looseWire -< oldBall
(newAmmo,blocks) <- blocksWire -< ballBlockColls `M.union` blockBulletColls
oldBlocks <- delay $ [] -< blocks
_ <- winWire -< (map snd oldBlocks)
(newBullets,gun) <- gunWire -< (fireRequests,newAmmo)
bullets <- bulletsWire -< (bulletBlockColls,newBullets)
oldBullets <- delay $ [] -< bullets
returnA -< Just $ GameState paddle gun ball (map snd blocks) (map snd bullets)
else
returnA -< NothingFirst the paddle is updated using the input. The fireRequests are build by accumulating all presses of the fireing key. These are later filtered in the gun, so that no more bullets are fired than there is ammo. When an Update event is issued the queue is purged. Remember that accum delays by one, so that when the input event is "Update", fireRequests is purged one invocation later.
The rest of the wire is only invoked when the input event is "Update" (otherwise Nothing is returned). Note that we can use "if" to invoke a different wire depending on some condition. Creating the collision data is done using the functions introduced earlier. Note the filter with "validCollDir". Due to the rounded edges, it can happen that the ball collides with a block in a way that the ball is not outside the block the next frame. To prevent "double collisions" all those collision events, that are not directed against the moving direction of the ball are filtered.
If we would have used "accum" instead of "accum1" in a couple of places, the output of all the game objects would be delayed by 1 and we would not need the "old..." objects. This is personal preference, I find the use of the "old.." objects more transparent to what is happening.
Conclusion
I am getting more confortable with haskell and its getting easier for me to read haskell code. Netwire seems to be a nice library, but I feel like I have so far only scratched its surface. I wonder what cool things one could do if one would use the inner monad. Also I wonder how Arrowrized FRP compares with FRP without arrows. Unfortantly reactive banana does not yet work with haste. I had a quick peek at elerea but it also needs some PrimOps not supported by haste.
Again: I encourage you to comment if you think something could be done better. For a lot of things I might not use a better alternative because I am simply not aware of it. After all I am still a haskell beginner.

Writing JavaScript games in Haskell by Nathan Hüsken is licensed under a Creative Commons Attribution 3.0 Germany License.